2020-02-24 – Teste a verificação de pontos e triângulos com colineariedade em C++.
Um post que partilhei com amigos em 24 de Fevereiro de 2020 de um teste que fiz de verificação de triângulos através de 3 pontos, por curiosidade deixo aqui. Está disponível na Internet o código.
«Um pouco de Matemática. 10 milhões de testes a cada algoritmo, mais de mil milhões de cálculos para testar algo.
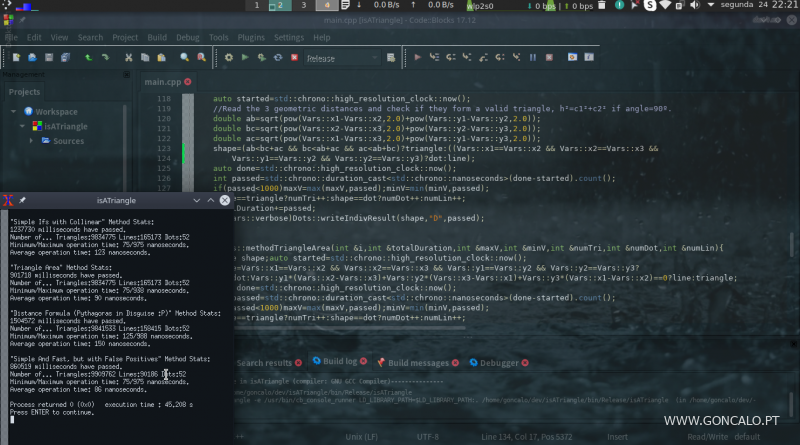
Criei um pequeno programita em C++ só para medir quais os métodos mais rápidos de detecção de triângulos através de 3 pontos. O método que referi a um professor é obviamente mais rápido, mas no teste apesar de mais rápido está atrasado com condiçoes, o do professor é o da distância, é o mais lento, e o mais rápido dos correctos é o da área do triângulo, e explico abaixo porquê, além de ter um criado por mim que dá falsos positivos mas fica mais rápido, com margem de erro de 0,5% apenas.
O do professor é o (como eu digo) “teorema de Pitágoras disfarçado”, o que vêem no código com h²=c1²+c2², esse é o que o professor defendia, e é muito mais lento em 10 milhões de testes, alternados (a+b+c+d+a+b+c+d+a+b+c+d) para ser igual para todos com as flutuações de ciclos de processamento do CPU, 20% a 60% mais lento que os melhores, com 150ms de média, e tem falhas, a rondar 0.1%, talvez por arredondamentos de resultados com vírgula flutuante. Tal como falei na altura, raízes quadradas é para esquecer.
O das slopes é uma verificação de colinearidade com 100% de certezas (daí ficar mais lento para 123ms), é 100% exacto, e mais rápido, tal como falei!
O da área é o melhor, muito exacto, podem ver que coincide a 100% com o meu da colinearidade, e baixa de 123 do meu para 90 nano segundos por operação, ao contrário do que o professor recomendou, cheio de falhas inerentes ao funcionamento dos CPUs (e por trabalhar com raízes quadradas), podem ver que em 10 milhões de valores pseudo-aleatórios o número de triângulos e pontos coincide a 100%.
E para certas operações mega rápidas, onde se pode permitir alguma inexactidão, como em vídeos, jogos, estatísticas onde 0,5% seja irrelevante, criei o “Simple and Fast but With False Positives”, a margem de erro é de 0,5%, e não compensa muito, poupam-se só 4 nano segundos por operação, 40 milhões de nano segundos no total, meio irrelevante, e perde apenas no caso de existir colinearidade diagonal que é raro neste caso.
Resultado:
Estava eu obviamente certo, a minha maneira de testar é 100% exacta e eficaz, e 100% coincidente com a mais exacta de cálculo de área de triângulo pelos 3 pontos (área >0 é triângulo obviamente), ambas com 123 e 90 ns, por vezes 110-90, u 100-80, e a do professor, com raízes, etc, é muito lenta (150ns), propícia a erros (raízes e problemas de números reais no computador, com as vírgulas flutuantes), e o com falso positivos, não compensa. ![]()
Há quem me pergunte se sou programador lol. Na realidade não sou só programador, faço 1001 coisas, A programaçao é apenas uma ferramenta útil para certos objectivos, e por isso tenho de a usar. Sim, devo ser programador, mas não me limito a isso, é apenas uma ferramenta, nada mais.
Um post que partilhei com amigos em 24 de Fevereiro de 2020 de um teste que fiz de verificação de triângulos através de 3 pontos, por curiosidade deixo aqui. Está disponível na Internet o código.
«Um pouco de Matemática. 10 milhões de testes a cada algoritmo, mais de mil milhões de cálculos para testar algo.
Criei um pequeno programita em C++ só para medir quais os métodos mais rápidos de detecção de triângulos através de 3 pontos. O método que referi a um professor é obviamente mais rápido, mas no teste apesar de mais rápido está atrasado com condiçoes, o do professor é o da distância, é o mais lento, e o mais rápido dos correctos é o da área do triângulo, e explico abaixo porquê, além de ter um criado por mim que dá falsos positivos mas fica mais rápido, com margem de erro de 0,5% apenas.
O do professor é o (como eu digo) “teorema de Pitágoras disfarçado”, o que vêem no código com h²=c1²+c2², esse é o que o professor defendia, e é muito mais lento em 10 milhões de testes, alternados (a+b+c+d+a+b+c+d+a+b+c+d) para ser igual para todos com as flutuações de ciclos de processamento do CPU, 20% a 60% mais lento que os melhores, com 150ms de média, e tem falhas, a rondar 0.1%, talvez por arredondamentos de resultados com vírgula flutuante. Tal como falei na altura, raízes quadradas é para esquecer.
O das slopes é uma verificação de colinearidade com 100% de certezas (daí ficar mais lento para 123ms), é 100% exacto, e mais rápido, tal como falei!
O da área é o melhor, muito exacto, podem ver que coincide a 100% com o meu da colinearidade, e baixa de 123 do meu para 90 nano segundos por operação, ao contrário do que o professor recomendou, cheio de falhas inerentes ao funcionamento dos CPUs (e por trabalhar com raízes quadradas), podem ver que em 10 milhões de valores pseudo-aleatórios o número de triângulos e pontos coincide a 100%.
E para certas operações mega rápidas, onde se pode permitir alguma inexactidão, como em vídeos, jogos, estatísticas onde 0,5% seja irrelevante, criei o “Simple and Fast but With False Positives”, a margem de erro é de 0,5%, e não compensa muito, poupam-se só 4 nano segundos por operação, 40 milhões de nano segundos no total, meio irrelevante, e perde apenas no caso de existir colinearidade diagonal que é raro neste caso.
Resultado:
Estava eu obviamente certo, a minha maneira de testar é 100% exacta e eficaz, e 100% coincidente com a mais exacta de cálculo de área de triângulo pelos 3 pontos (área >0 é triângulo obviamente), ambas com 123 e 90 ns, por vezes 110-90, u 100-80, e a do professor, com raízes, etc, é muito lenta (150ns), propícia a erros (raízes e problemas de números reais no computador, com as vírgulas flutuantes), e o com falso positivos, não compensa. ![]()
Há quem me pergunte se sou programador lol. Na realidade não sou só programador, faço 1001 coisas, A programaçao é apenas uma ferramenta útil para certos objectivos, e por isso tenho de a usar. Sim, devo ser programador, mas não me limito a isso, é apenas uma ferramenta, nada mais.
PS: Não perdi tempo a simplificar demasiado o código e meter comentários. ![]() E sim, está bem, o C++ não é tão simples quanto a porcaria do Python, mas é 1000 vezes mais poderoso e rápido.
E sim, está bem, o C++ não é tão simples quanto a porcaria do Python, mas é 1000 vezes mais poderoso e rápido. ![]() » (2020-02-24).
» (2020-02-24).